Juan Sánchez-Baena defiende su tesis sobre correlaciones en sistemas cuánticos ultrafreds con acoplamiento espín-órbita

La evaluación de los efectos de las correlaciones en sistemas cuánticos es una tarea laboriosa a causa de la imposibilidad de usar aproximaciones de campo medio al resolver la ecuación de Schrödinger. A fin de cumplir este objetivo, se presentan dos prescripciones: la elaboración y utilización de métodos de Monte Carlo y la realización de cálculos más allá de la aproximación de campo medio con la técnica de Bogoliubov-de Gennes. En cuanto a la primera opción, se muestra como adaptar el método de Monte Carlo de Difusión (DMC) estándar para samplear adecuadamente interacciones espín-órbita. Se desarrolla el formalismo de propagadores para dos métodos diferentes capaces de lograr este objetivo. Este dos métodos son el Discrete Spin T-moves DMC (DTDMC) y el Spin-Integrated DMC (SIDMC). El primero, el algoritmo DTDMC, se corresponde a una adaptación de un método previamente existente a variables de espín discretas. Este método requiere de la definición de un Hamiltoniano efectivo para curar un problema de signo, lo cual reduce la calidad de sus estimaciones. Por otro lado, el segundo método (SIDMC) es un algoritmo completamente original desarrollado en este trabajo. Este método es capaz de ignorar la definición de este Hamiltoniano efectivo por medio de la propagación en tiempo imaginario de la función de onda integrada sobre el espacio de espines. Como consecuencia, la calidad de las estimaciones obtenidas con el SIDMC es superior a aquellas obtenidas con el DTDMC. No obstante, el SIDMC es incapaz de samplear interacciones a dos cuerpos que dependan del espín. Usando el método DTDMC, se elabora la extensión del diagrama de fases de un sistema con espín-órbita Raman al régimen correlacionado. Los resultados muestran que las correlaciones favorecen la exótica fase con modulaciones de densidad, la fase stripe, que abarca una extensión del diagrama más grande cuanto mayor son las correlaciones. Además, se reportan resultados para la función de distribución de parejas, el factor de estructura estático, la matriz densidad de un cuerpo, y se caracteriza cuantitativamente la superfluidez de esta fase, mostrando una fracción superfluida no nula en la dirección transversal respecto a las modulaciones de densidad.

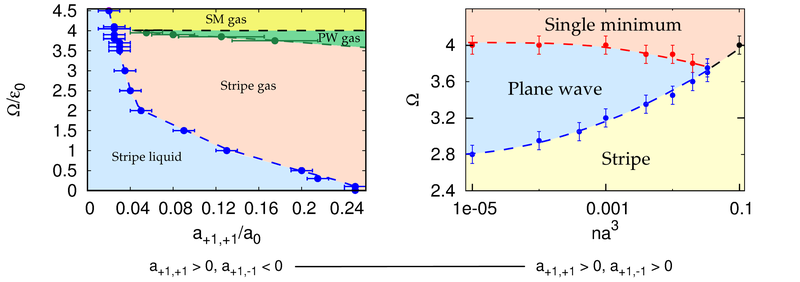
En cuanto a la segunda prescripción mencionada previamente, se ha seguido el formalismo de Bogoliubov-de Gennes para realizar cálculos analítico-numéricos que tengan en cuenta las correlaciones a primer orden respecto a un cálculo de campo medio para un sistema con espín-órbita Raman. Esto ha permitido obtener la corrección de Lee-Huang-Yang (LHY) a la energía de campo medio para la fase stripe de este sistema por primera vez. Usando este resultado, se ha podido determinar el papel que juegan las fluctuaciones cuánticas en un sistema en la fase stripe que es inestable a nivel de campo medio a causa de la presencia de interacciones entre componentes de espín suficientemente atractivas. Actualmente, estos sistemas se encuentran en desarrollo experimental. Los resultados muestran que las fluctuaciones cuánticas estabilizan el sistema, y dan lugar a una fase líquida o gas en función del valor de los parámetros del Hamiltoniano. Además, el sistema finito soporta la existencia de gotas líquidas auto-ligadas como estado fundamental. Estas gotas muestran modulaciones de densidad inducidas por la interacción espín-órbita. Por lo tanto, representan un estado de la materia novedoso en el campo de los gases cuánticos ultra-fríos, puesto que presentan una combinación de propiedades de líquido, de sólido y superfluidez. A fin de facilitar los cálculos de la corrección de LHY, se reporta un funcional fenomenológico que reproduce con precisión los resultados provenientes de cálculos completos.

Finalmente, también se reporta un breve análisis de un sistema cuántico de muchos cuerpos con acoplamiento espín-órbita de tipo angular. Se reporta un estudio con DTDMC del impacto de las correlaciones en un sistema de este tipo. Los resultados muestran que la aproximación de campo medio es capaz de predecir con precisión las propiedades del sistema para el rango de parámetros considerados.